From elevator music to causal thinking

Today, I'm going to be the person who believes everything shown to me in the office building's elevator.

According to some study, they claimed that drinking sparkling water can help people reduce weight - but only if drinking it is combined with having sufficient exercise. (This went by fleetingly so I'm missing part of the paragraph.)

The scientific claims can be stated as:

• Drinking sparkling water by itself does not lead to weight loss
• Drinking sparkling water in addition to exercising leads to weight loss

So, if we trust that they did a proper study, then we should be stocking up on sparkling water while also renewing our gym membership.

That sounds like a reasonable action plan that takes advantage of the study's findings.

Wait, but we are ignoring another plan that is also fully consistent with those two points. Namely, that we just renew our gym membership.

That's because we don't have information on the following:

Does exercising alone lead to weight loss? (Presumably yes). Does exercising plus sparkling water lead to more weight loss than exercising alone?

***

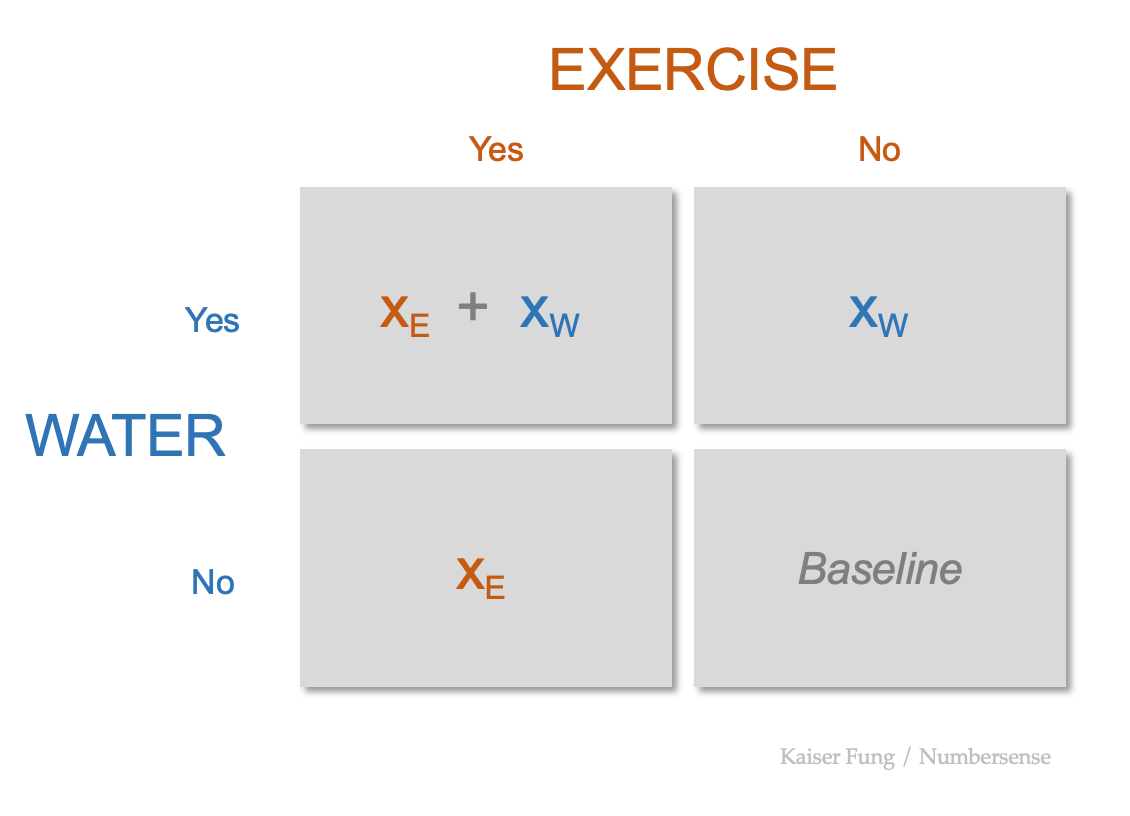
We can set up the following grid:

The elevlator blurb provides information about the top left cell. It's saying the total effect of both exercise and water is positive in a meaningful way.

Our first question concerns the bottom left cell - is the contribution by exercising positive in a meaningful way? If yes, then we'd like to know what proportion of the total effect it accounts for.

If exercising has no effect, then the total effect is just the effect of drinking sparkling water. If exercising has a negative effect, then the total effect under-estimates the effect of water alone. Both these cases can be excluded since we were told that water alone is insufficient.

The two claims lead to x(w) is close to zero, and x(e) + x(w) is dominated by x(e).

If most or all of the total effect is due to the effect of exercising, then the claims above are "true lies". While it is true that the total effect is important, most of all of the effect is due to exercise, and not drinking water.

***

The grid above uses a very simple model typically found in many medical studies but it's a overly simple model. Let's look at a more realistic grid:

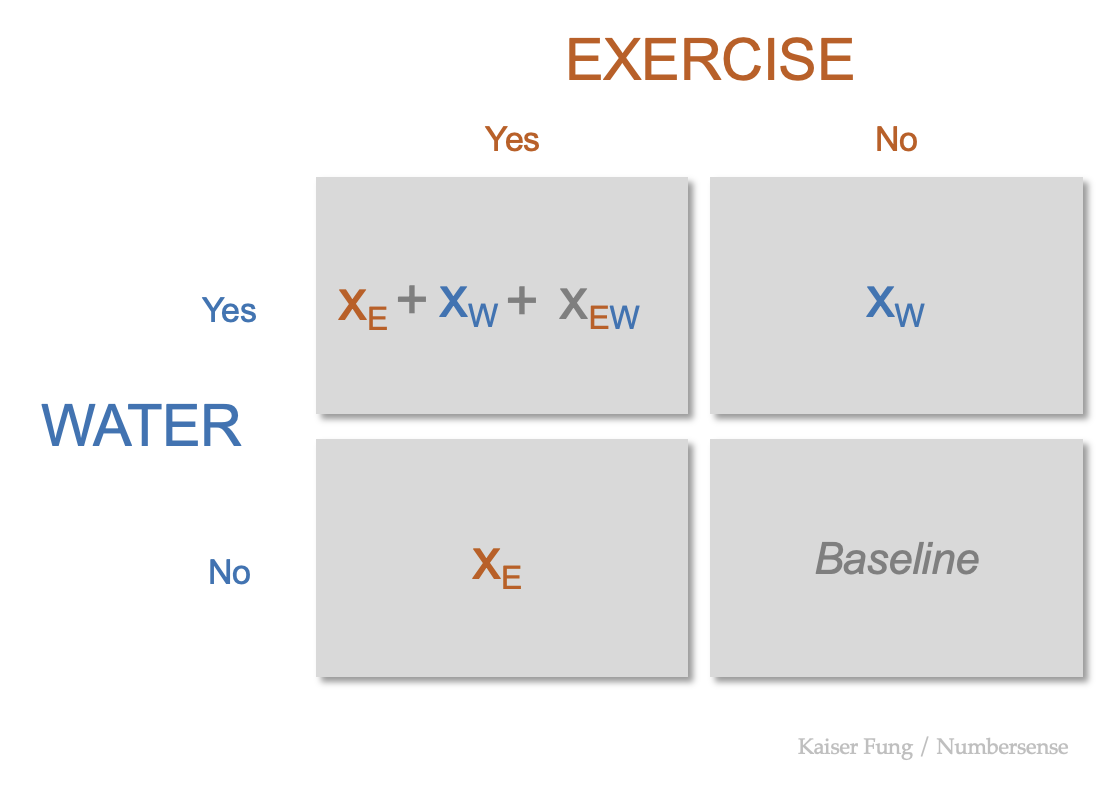
The key change is the quantity inside the top left cell. Previously, it's the sum of the individual effects. Now, the sum is modified by an additional term called the "interaction effect", which depends on the values of the individual effects.

The interaction term enables synergies, positive or negative. The sum of 2+2 can now equal 5 or 3 whereas in the first model, 2+2 = 4 always.

For positive synergies, the total effect is larger than the sum of the individual effects; for negative synergies, combining the two effects results in a smaller total.

***

Let's consider this possibility: drinking sparkling water by itself is useless but drinking together with exercising triggers some special synergy, indicated by the fact that the total effect is larger than the effect of exercising alone. This scenario is not admissible in the first, simple model described above.

Let's clarify why the second model can capture reality better. Let's fix a model of the interaction effect, x(e,w) = k x(e) * x(w). This says that the modification term depends on the product of the individual effects, plus a factor k (which can be any number or fraction).

Under that model, we can see that the total effect can be written as x(e) + x(w) [1 + k x(e)]. This means that while the effect of water alone is x(w), the effect of water in the presence of exercise is x(w) modified by a factor, and that factor's value depends on the effect of exercise. Simplified, we're proposing that the effect of water varies based on the effect of exercise.

Similarly, we can write the total effect as x(w) + x(e)[1+ kx(w)], and confirm that the effect of exercise varies based on the effect of water.

In the first model, the effect of water is always x(w) regardless of exercise, and the effect of exercise is always x(e) regardless of water.